Natural Systems Design Science

 Jessie Lydia Henshaw  -  AAAS - ISSS

- noticing broad patterns of design in the complex organization of natural systems -

 Google Scholar, Publications, Journal - Reading Nature's Signals, Contact - sy-at-synapse9-dot-com

HDS is a small center for research and consulting on patterns of organization and design found in studying natural systems of all kinds.  In short, its application is then systems biomimicry, learning from observed systemic designs, constructive and destructive, for improving our designs. The study demonstrates that we really can understand some of the familiar complex and holistic transformations that enliven life and also give us terrible problems. Common life tasks of "growing up" or "making dinner," for example illustrate what we are failing to do with the world economy, starting with system innovation and ending growth with system coordination:

like any kind of work needs to do to provide good service in the end.

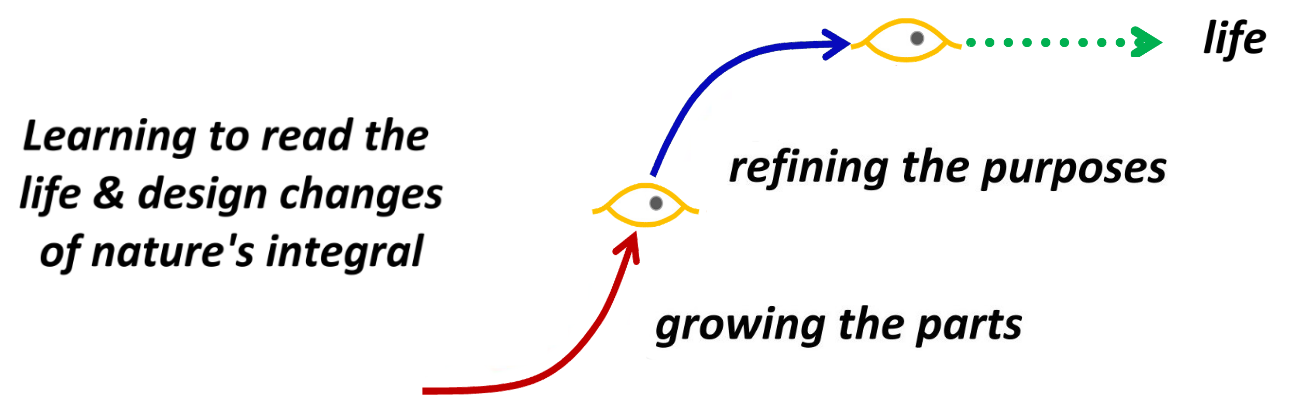
That feature of natural growth seems to define nature's universal system-development process, started with - an innovation for capturing resources with positive feedback for capturing more - shifting to a positive feed-forward for coordinating internal and external relationships - represented below as an S curve called "nature's integral, " (i.e., how things add up). That makes the HDS approach one of studying common experience for design patterns, as well as ecology, general systems, natural sciences, and architectural design practices such as "pattern language" for ways in which systems thrive or fail. What's special about the shape of "nature's integral" is not the S symbol, but its uses as a guide-map of transformation in complex systems. As it embodies one of the great logical contradictions of growth curves, switching the signs of the internal development - in response to internal and external contexts not shown - in the middle of the growth process. It help a lot for turn ones attention to the the contextual territory where the authentic behaviors of complex natural transformations are taking place. The red-blue-green periods represent three successive system designs in that case, that we are all rather familiar with in our daily lives. As emerging systems develop (eventually to last for long or short periods), that go from building up the parts in relation to the starting design to then refining their interior and external relationships and actual or implicit purposes, that we use without thinking all the time.   The crucial step is at the midpoint, where the positive feedback of the red line turns into the life-affirming feed-forward of the blue line.

 jlh eds 4/14/22 -

Jessie is currently active in the ISSS evolution of systems science and thinking with a paper on how natural systems need to begin with a continuity of forms of organization and what nature's apparent purpose in starting growth with a formative period of positive feedback seems to be.  In preceding years she has gone back to writing papers as her new perspective jelled, following on her observations from years of learning how people see the complexities their problems, at the UN and in extensive correspondence.

From 2012 to 16 she was active in the development of the UN's SDGs and supporting the systems thinking in the evolution of sustainability programs at the UN and with the UN's NGO Major Group and other organizations. Though learning more about the barriers than the openings, the work made small but important accumulative steps toward a common recognition of our global problem. It seemed for a while that 2020 would be the 20-20 "year of clear vision."   The red line in the diagram would represent our ~250 year period of rapid global growth, and the blue line our perhaps next 250 years of learning what to do with it, as we refine our design for civilization for the coming climax phase of our life on earth, i.e., a 'good' thing to do.

Eds 1/21/13, 4/9/16, 4/18/19, now needs update -  So the starting point for any client with any large or small challenge to face, is to recognize nature's integral in their ordinary experience, like making lunch, or pouring a drink, and then in bigger and more complex transformations too, such as starting and completing any office project, or leading a confused planet to safety.  From a natural systems view the same general map of transformation is always where to begin exploring its many variations.  The model is not magic, more of a suggestive notepad for a do-it-yourself plan, that keeps asking you "and then?" in a way that keeps your attention on the stages of the making any transformation whole.  So it does not always work, of course, or follow a simple path, but when it works, it does always start a continuity of growing the parts then refining their purposes, to end at a point of completion and independent life.

Jessie is an independent physicist and architect who developed this as a new general science of systems ecology.  It originated with field studies of the physics principles and evolving design patterns of emergent organization in nature, concentrated on the designs of convection. She's been proposing ways for the economic system to transform and become sustainable since discovering in the 1970's the close corollary between energy in nature and money in the economy, and then finding that Keynes discovered the same principle, which he called "the “widow's cruse."  Her discovery that you could (and should) think of natural systems as working by themselves was what opened the door.  That profound shift in perspective, to considering nature as working by itself rather than by our information, led to many verifiable and useful discoveries that differ from expectation.

Seeing nature as working by itself, not by our information, leads to applying science in a new way.  Scientific inquiry then starts from recognizing nature's flows as evidence of environmental organization rather than the opposite, taking all data out of context to use for creating equations and representing the equations as nature's organization.  It's a difference between studying nature's things and studying our own rules.  One developed technique is the adaptation of Christopher Alexander's "pattern language" as a language of design for holistic environmental transformations.

Jessie’s work is published in research papers, her RNS journal of research reports, and her archive of experiments. She was born in 1946, growing up in Hamilton NY, and now lives in New York City.   She received a 1968 B.S. in physics from St. Lawrence University, followed by some postgraduate study in mathematics at Stony Brook and Columbia, and then a 1974 MFA from the Univ. of Pennsylvania in architecture, landscape, and micro-climate design. Her many years of independent research then began when moving to Denver and making her first important findings studying the natural micro-climates of homes. She has since continued to accumulate a body of useful new work.  
 

Research Archive: synapse9.com/   

RNS journal: Reading Nature’s Signals – synapse9.com/signals  
Publication & Resources – synapse9.com/jlhpub.htm   Consulting resume – synapse9.com/jlhCres.pdf

_________________________________________________

The following is a bit out of date, a slightly older viewpoint perhaps of interest.

To study natural systems one considers them as having developed from usually unnoticed beginnings, by building on the origin pattern of design that starts their development. So they appear to us as “found objects of design” in the environment, recognized by the organization of their parts, and by both how their organization is continually changing and operates within its self-defining organizational boundary.   The lasting rules they follow are very general, such as that their organization is invariably accumulative and built on what went before, by joining opposing shapes generally, and developing by a succession of "non-linear" organizational stages, first building up then building down.  We use our familiar experiences of life as metaphors or examples of these successions of natural design, "pregnancy" corresponding to the explosions of innovation beginning from a tiny seed pattern, and "maturity" as a long process of perfecting what pregnancy creates.   Other patterns of the same succession include how a business start-up always begins with a seed pattern and goes though a period of relatively dangerous radical innovation and development, to spend years refining the service, craft or product being produced.  It's a model that applies to almost any design of life that comes to matter to us, an invasive growth of some pattern in one environment, that then either finds or fails to find a stable set of roles in the discovered environment it grows into.

What makes it a particularly complex subject is the difference between discussing the "temporal processes" and the "spatial designs".  We see them so differently that they need to be discussed in different terms, but understood as connected all along too.    The timeline of natural designs is a story of accumulating innovations that may go back and forth between periods of increasingly radical innovation (the periods of compound growth) and periods of refinement and perfection, of the designs the radical innovations produced.   The familiar occurrence of that is the succession of "graduations" we experience in going through successive stages in learning, requiring alternating radical expansions in thinking and periods of (somewhat) perfecting it.    How the connections of new things build on the starting pattern that form those somewhat predictable successions are what one studies.  It leads to understanding how the working parts work, and are changing.   In general any rule one finds is likely to be temporary, because... it's 'life'.   

The most common reasons for systems to break their own rules is either 1) becoming connected or disconnected from others or 2) changing scale, either getting too big or too small for their prior way of working to work.   The "resilience" of excess duplication in working parts and surplus resources, that all systems need so they can maintain themselves despite unexpected shocks or limits of change, then works to maintain continuity when something has to change, assuming a bridge of new design or resources is found.  So, understanding that we can admire the seemingly magical processes of natural growth and decay and peer into what actually going on, and what the stakes are a bit.  

__________

jlh 1/21/13, 4/9/16, 4/18/16