,
, 
,
of great transformative changesshapes found in time traces, displaying the continuity formed by the cascades of change, serve as a guide map to creation and extinction.
,, ,
of great transformative changes)
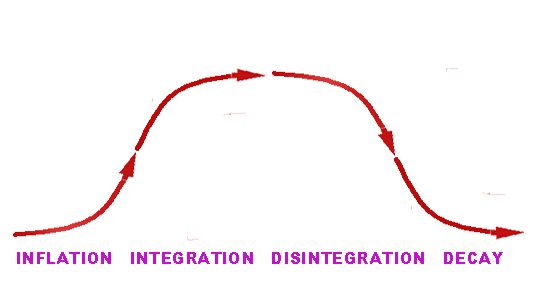This
idealized elementary sequence of growth dynamics, tracing change from beginning
to end, represents the most common and fundamental of the complex
dynamics to be found. The set sequence of shapes reflects a set sequence
of local complex systems, arising from some small beginnings, concluding
in small ends. Each stage represents a separate necessary evolution
of complex processes which may appear as simple as a bump on a curve, a
heart beat, a storm, an epidemic, a thought. Compare
the model to something familiar to you, the course of your own emotional
experiences or endeavors, the course of simple physical events like a single
spark, a sound or a life. Any event which can be traced from beginning
to end can be informed by this model guide map to creation and extinction.
Don't let it fool you that passing events displaying this same shape are sometimes predictable from remote conditions. The physical means of change is still required to bring them about whether the outcome is predictable or not. Change arises and subsides by way of locally evolving mechanisms. What we can most easily observe is that all change starts and ends with accelerating change, which then decelerates. It reflects complex systems which do the same. In some cases, as ideally represented here, these four complex processes occur in succession, as separate processes. The shape of the curves is simple. What makes them complex is that complex local networks of physical processes are needed to bring them about. The underlying complex mechanism is reflected in whatever measure you choose to trace, providing corollary information about the central mechanisms.
Please let me know what you think JL Henshaw
Inflation
[Growth] (+e^+; positive exponent increase; accumulating order with positive feedback
of outputs to inputs) This is generally the first observable beginning
of change, a cascade of local effects by which significant structures develop.
It is how things begin in the absence of the rules and structures which
are to develop. What we observe are successive steps that are
multiples of prior steps as a local system of interactions widens, differentiates
and develops. A spark develops by an inflationary cascade of ionization.
A blink of an eye develops by an involuntary inflationary cascade of
nerve impulses. A summer storm develops as an inflationary
cascade rising air currents. An inflationary cascade of particle
formation apparently occurred as the mechanism by which the universe developed
and differentiated.
Integration
[Stabilization]
(+e^-; negative exponent increase; accumulating order with negative feedback
of outputs to inputs) An initially inflationary system may change and approach
a climax state of steady operation. One might also call this phase
'maturation' or 'refinement' because it represents the shaping of the original
inflationary system into a steady state system. The maturation of living
things or the maturation of businesses provide good examples of the transition
from compound growth to stabilization. As with a flame which first
grows and then reaches a climax, many examples of stabilization represent
resource limitation. Think of examples familiar to you, a maturing
business plan, plant or ecology. Self-sustaining mechanisms
and stable structures develop by smaller and smaller steps toward a local
perfection of their system.
There are also those which never stabilize, but only continue inflationary growth to a point of either their own internal collapse or an abrupt exhaustion of their resources. A rocket engine is a good example of a flame which grows explosively but then reaches a steady burn rate, ending its inflationary period of development just short of ripping itself apart. We hope humanity does at least as well in minding the inflationary growth of our impacts on the earth.
Steady
State (balanced outputs to inputs, homeostasis) is the
product of maturation. Regular rules and expectations apply, even
though the system involved may be exceedingly complex. We simply
do not need to be concerned with its complexity to predict its behavior.
That can not be said about the other types of developmental progression,
which is part of why they remain mysterious. During Integration
and Decay the outcome may become clearer as time progresses.
During Inflation or Disintegration both the immediate and
long term behavior may be quite hard to predict, and become less predictable
as time passes.
Disintegration
[Collapse](-e^+; positive exponent decrease; accumulating disorder with positive
feedback of outputs to inputs) That relatively quiet time when things start
falling apart usually goes unnoticed, only to catch us off guard as its
disorder multiplies. What often seems impossible from the view
of a steady state in none-the-less inevitable, as all things must pass.
Whole industries begin to disappear, little noticed, as attention and resources
are diverted elsewhere and as their misfit with current trends becomes
more pronounced. The disintegration of a family or political
regime proceeds from small errors to large catastrophes.
Materials which first show signs of wear then more and more rapidly disintegrate.
Decay
(-e^-; negative exponent decrease; accumulating disorder with negative
feedback of outputs to inputs) is the end of all things. It proceeds
by successively smaller steps as the components of the former process are
dismantled successively smaller and smaller steps.
back to Observing Dynamics
ed. 6/1/01