Models Learning Change
Feb, Mar, 2010
Connecting theoretical systems to the natural
world of complex systems
P. F. Henshaw, HDS complex systems science
680 Ft. Washington Ave, NY NY USA,
tel & fax: 212-795-4844, email: eco@synapse9.com
[note: This is a draft of essay to be published in Cosmos and History
June 2010 Models
Learning Change (author copy)]
Abstract
Because
"the map is not the territory" it's valuable to learn how to watch
the territory to see when to change your maps of it. That is can be
foreseeable and important for our maps of the irreversible processes that lead
to natural systems changing form. They're signals that new maps
will be needed. For theoretical models it serves to replace
equals signs with question marks at times of change, prompting you to look for
new assumptions and rules of the road as they emerge.
Theoretical
models can be complete abstractions, or based on information to represent
states of physical organization in some individual physical system.
Those that have physical subjects are valid as information about
their subjects only if people use them with a wider understanding of the
complex nature of the real subject and its real environment. Models
can describe all kinds of feats of change that physical systems are unable to,
and physical systems can do all kinds of feats that abstract models can't, like
change by themselves. Anticipating such change in the
organization of physical processes prompts searching for new information and
adapting the models. A method for doing so follows from how the
conservation of energy limits the kinds of change that are physically possible.
In practical terms, for lasting change to begin or end, the conservation of
energy requires that it's energy flows not have instantaneous leaps, and so incorporate irreversible developmental processes
of accumulative change, such as growth and decay. These can serve
as markers for anticipating changes in form for the physical systems that
display them, and be ready to adapt the theoretical models that describe
them.
These
signs of irreversible change can be empirically located by their observable
mathematical signatures to determine by observation if there are complex growth
and decay processes associated with them. A practice of
watching both models and environments for such processes of irreversible change can then help maintain a connection between models
and their subjects. It can provide added time for effective
response to changes arising from the complexity of the physical system beyond
the information in the model. It's especially valuable for learning
how to respond to the behavior of natural systems with independently learning
parts. They change direction according to what the parts are
learning, not any map or model at all. The unpredictability of what
the parts are learning may be highly consequential so early understanding quite
useful.
Science
has not usually maintained a duality between information systems and physical
systems, though, except to refer to physical systems as
'undefined'. That would then mean restricting terms like
"system", "organization" or "object" to
exclusively apply to the world of theory and information, and relate to the
world of physical things with no particular reference to them, except
data. Here "physical things" are referred to as
existing prior to any information gathered about them and to be observed as
individuals somewhere in particular. "Information" is
implicitly defined everywhere in general but is solely a human construct and
meaningful only within the culture of those that invent it.
Human language, though, did not originally arise from information, but for
referring to the things of the physical world around us. Presently
language often confuses the distinctions, though. So, though one
cannot refer to organization in physical things as made of information as
organization in our models is, it's quite possible to refer to and study the
physical organization of nature as a subject, and keep the two quite usefully
distinct.
Whether
one is referring to information or to physical things mostly needs to be
understood from context. That is aided by studying the major
differences between what information can describe and that things can
do. Theoretical models depicting physical systems are necessarily
self-contained in their own unchanging definitions, and are also necessarily
represented as existing in isolation without an environment. The
person who uses a theoretical model needs to supply the rest of the
relationship between the model and the physical subjects it points to in the
world. Natural physical systems, in contrast, are complex beyond
the reach of information and arise from within an open environment in an
undefined way. They also continually change everywhere at once
without having a way to apply general rules from somewhere else. These are
quite large differences. Models and things can fit each other
loosely, as between the weather and weather forecasts. For
some subjects they can fit snugly, as between hand and glove.
An
example of responding to natural change in the physical form of economic systems,
and in the models and "rules of the game" implied, introduces a
discussion of the window of opportunity for doing so.
Keywords:
scientific method, mathematical modeling, physical systems, models,
learning, change, adaptation, foresight
Working draft - mostly 9/2/09
1.
Introduction
The
understanding of natural systems found embedded in open environments and
changing form continually, has been limited by representing them with
theoretical models. Natural systems display local organization that
accumulates as an environmental learning process around the movement of energy.
Models are useful for times when natural systems are regular, but
cannot predict complex organizational change, or environments.
That and other inherent differences between theoretical models and
natural systems can be exploited to train researchers to adapt their models to
changing physical organization they otherwise could not predict.
All
physical systems have natural limits of scale, for example, and models tend not
to, so systematic progressions of scale predict physical system changes to look
for that models will not reflect. Some difficulty arises in
overcoming the language problem of discussing differences between physical and
theoretical systems. Normal discussion frequently refers to
both mental abstractions and physical things with the same terms, as with the
word “apple”. Normal usage is to use words to refer to both our
ideas and information about a subject, and the
physical thing with features beyond our information at the same time as if to
not distinguish.
The
method proposed here is to develop indicators for when to look for changes in
physical systems that require model changes beyond the information previously
available. It provides timely indicators for when to change
assumptions and some general indication of how. It does not offer
the "holy grail" of modeling, to define the systems of nature, but
helps give apparently vague forms successively clearer features and allow our
fixed rules and definitions to fit them more responsively. It is
not always successful but it generally exposes productive questions that would
not be asked otherwise. The particular strategy to be proposed is a
way to represent processes of regular proportional change as having both
different organization and environments at their beginnings and
ends. That prompts, or you might say 'forces', one to pay attention
to the interior details of complex autonomously changing systems that models
are so useful for ignoring.
What
models and explanations do for us, where we get them to work, is represent one
scale or regular aspect of organization, assuming the regularities of others
are constant. That helps predict what those regularities would
result in, but is valid only as long as those assumed constant properties
remain so. That assumption is always highly uninformed, is the key, a
matter of faith. Due to the natural complexity of physical things most of
what is assumed constant is completely unknown, so we can't possibly know all
of what we assume. There are useful indicators of when some assumptions
will certainly need to change, though.
For
example, if you have a simple computable model of ocean waves, changing the
scale of the variables does not change the behavior of the model.
Increasing the scale of actual waves leads to a point where they break,
however, due to physical system scales not represented in the model. That
difference in behavior due to scales of organization that models contain no
information about, is itself predicable. It helps predict the emergence
of new realities and lead to discovering them, whether the circumstance
concerned is familiar or not. In that case it raises the certainty
that the old model will not continue to be valid.
The
usual aim of modeling is to finding what regularities can be relied on.
The interest here is rather the opposite, what regularities can be relied on to
fail. It's like a "check engine light" for environmental
models. The object here is to exploit common regularities certain
to be temporary for pointing to what parts of a system will change for reasons
beyond your present information. That can help locate where change has or
will occur to raise good questions about the missing information needed.
The
learning isn’t over when a good set of regularities and a useful model are
found, but really just begun. Learning how to use models to help
anticipate natural system changes would teach a great deal about how to adapt
to or avoid conflict with them. Because natural systems are learning
processes themselves, requiring coordination of environmental changes and
complex responses, there are hair raising complications of trying to change them
ever more rapidly, complications not found in models.
The
issues are framed in a conversational style both for wider audiences and
because the real subject is a new scientific method for raising
unanswered questions, a hypothesis generator as it were. A
scientific method not designed to produce equations, but to raise better
questions, is unusual. It might benefit from revisiting
issues from various perspectives. After discussing the main conceptual
problems and describing the method, a conceptual application addresses what
constitutes timely decision making about approaching changes in kind for
natural systems and the models used to represent them.
2. The basic
method
If
one can identify systems that are naturally temporary it raises the question of
how they begin and end. Beginnings like either the germination of a seed,
a handshake between people or the tipping of an environmental balance, are
events on other scales of organization than the processes that develop from
them. Process ending events are similarly different from the processes
they end. They include the slight jerk that occurs as breaks bring a
vehicle to a stop, the death of an organism, the completion of a task, and a
circuit burning out from increasing load. They are organizational events
on other scales than the subject process as beginning events are. As you
learn to look for them you recognize the kinds of processes that begin and end
with them, and it develops foresight for what to expect and what processes are
naturally temporary because of it. Processes that are necessarily
temporary include regular positive feedback systems. They begin somehow
(with smaller scale processes) and lead to conditions that make them end somehow
(with smaller scale processes). Watching for them leads one’s questions
beyond the information available to unexplained but connected processes and
relationships, and so to a path of inquiry where you can be sure of there being
information to find. The ability to predict them helps you to find them
and serves to expose other scales of system organization to view. Simple
temporary processes include the four types of systems of regular proportional
change, which are usually present where you find evidence of regular proportional
change (Fig. 4).
Fig.
4 growth ![]() | integration
| integration ![]() | disintegration
| disintegration ![]() | decay
| decay![]()
For
example, in studying plants you discover they come from the germination of
seeds, and that the end of their explosive seed growth is when they use up
their seed resource and switch to growing responsively to their environments to
begin their maturation. One needs to validate that any curve that looks
like regular proportional change represents a system of proportional change to
use this approach, of course. There are a variety of mathematical tests
to help verify the apparent systemicity of apparent
developmental processes as part of that (Henshaw 1999, 2007). As with any
search what you find depends on the combination of what is there and how
resourceful in looking for it one is.
As
with testing a hypothesis, the validity of each question is then to be
confirmed by having it lead to useful discoveries about the system producing
the evidence. Because feedback networks that are dominant enough to show
in measures of accumulative change tend to be system-wide, finding them also
tends to clearly localize the boundaries of individual system networks that are
acting as a whole and that is often a useful way to validate the original
question about them. The powerful question is asking how each kind of
system of proportional change begins and how its own development will lead to
its own end. As such it is also a new way of considering time, organized
as a one-way ladder of accumulative change by locating some of the rungs.
If
a system model itself implies either continual growth or decay for a physical
system, or an inflection from growth to decay, learning to read those as a
question about the implied behavioral changes in physical system is the
task. In each case once you’ve identified the likely behavioral change
approaching then that would probably lead to changing the model at some point
to correspond. Though the physical system features hidden from view one
looks for remain quite undefinable, this exploratory
approach still leads you to more and more details of how they are organized and
discovering better and better questions about them.
Chained
together as they commonly occur in nature, the four temporary systems of
regular proportional change become a general map of “how things come and go”
and “a typical life story” of developmental processes and their punctuating
smaller scale events. Fig. 5.
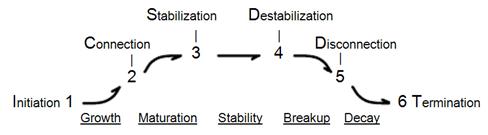
Fig 5. A Model of Change, six punctuating smaller scale events and five periods of regular proportional change. Showing one possible naming convention for the natural sequence of developmental processes (Henshaw 1985, Salthe 1993)
In
any case of either a model or an observed physical process exhibiting the
character of any place on the model of change prompts the questions about how
the physical system would be connected to the other parts and where in the
model to replace the “=” signs with “?” marks.
3 Conceptual
application & discussion
Keeping
with the conversational format the example application is discussed in relation
to the following diagram of alternative paths for a system making a switch from
growth to maturation, either early or late. The change symbolized is from
having a limitless environment and changing in proportion to itself to having a
limited environment and changing in proportion to its distance from its limit,
fig. 6. The equation is the same for each, with only a different
point in time for the switch from responding to the past to responding to the
future. It is almost self-explanatory that delayed response results in
disruptive change and timely response in smooth change, but it helps to see it
visually too.
Arbitrary
units are used and the response rate of 10% is used before and after. An
arbitrary point of failure (the Cap = 75) is set at 2.5 times the
arbitrary stable limit set at 30, as well as to to
keep the graph small enough for the page. What varies is the time when
switching from multiplying to limiting accumulation occurs.
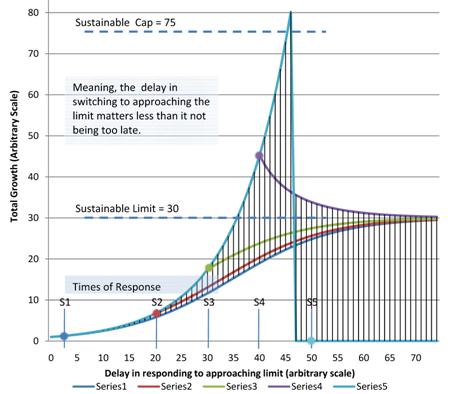
Fig. 6 - Growth toward a limit with delay in recognizing the limit: IFY0<cap,Y1=Y0*(1+RateConst*(1Y0*(IFBefore=0,else=1/limit)))
The
model represents any growth system as it changes from its independent seed
growth, and then switches to integrating with its environment, as in
maturation. The question asked is how does it affect
the system if the switch in response occurs early or late, with the time of the
change marked for each series. The clear implication is that switching
early has little effect on the future and switching late has a very large
effect.
One
need not know anything more to acknowledge the general principle displayed,
that in environments presenting a need to respond to new conditions the window
of opportunity for responding gets shorter and shorter. The important
recognition is that system response problems are all about the fact that
systems start without the information that a responses
will become needed. The practical opportunity is that the simple
information that the starting process will end does provide the information
that responding to the end will be needed. The model shows generally how
the timing of beginning that response determines whether it will be made
gracefully. The key is contradiction implied, that systems growing
independent of their future constraints need to “encode and decode” information
about a world of relationships they have no information about, before they make
contact. If systems don’t have information about the future, how do so
many seem to demonstrate exceptionally graceful self-limiting development. The hypothesis here is that it is by the
growth system itself becoming increasingly sensitive to disturbance as the
progression of the whole pushes its unseen parts beyond their organizational
limits, producing instability of the
whole.
Once
a system is sensitized to the need for change, brought on by its own internal instability,
the continuity of the process requires time for change. For people
involved in steering growth system responses to environmental limits the
difficulty is that the momentum of institutional habits from the past seems to
necessitate going well beyond the point where changing directions of
development cannot be made gracefully. That is the default case for when
the sensitivity to the need to respond did not come early enough. That’s
where the inherent temporary nature of systematic change needs to be the
information needed for drawing the conclusion that you need to prepare to turn
already, long before any contact with natural limits is made. Many kinds
of natural systems that gracefully respond to limits seem to do just
that.
The
trick seems to be needing to start to turn before you
really need to, otherwise the time needed to adapt to new conditions would make
a system unable to or to not do so smoothly. For example, as in paddling
a canoe on a winding river (or generally for any craft of steering) you quickly
discover that taking the last possible opportunity to turn risks capsizing and
spoiling the trip. So the earliest opportunity that is not premature is
the one you choose. That means being very sensitive to the need to steer.
You’d take the earliest opportunity to think of how to turn and then focus
attention on determining the optimal time to do so, ready to turn before the
need to turn, and particularly before the turning point is determined by
external forces. In the real world we have a choice just like that, the
need to steer our economic system with it’s
practice of adding to things by %’s built into the culture, practice,
projections and needs of society. It’s not even yet discussed in public
whether there is a question of needing to end the institutions of growth
somehow, let alone have a ready response for doing it. In responding to
the limits of growth the question of delay seems to be in how late we are in
seeing the need to turn at all. We seem likely to be following a path
like series 3, 4 or 5. Series 1 or 2 would have made the most graceful
turns, but the noticeable resource strains and series of major growth
disruption crisis for systemic causes suggests the system has already gone past
the period of unfettered growth it is thus already too late to climax smoothly.
For
people, understanding how to respond to limits is complicated by how the limits
themselves always seem moveable, allowing us to use our creativity to make
successive delays in dealing with it. The need to learn how to turn
doesn’t go away, but can be successively ignored, making the question one of
whether to respond to “soft signals” or waiting for “hard signals”. With
increasing effort and creativity it starts off being fairly easy to disguise the
mounting difficulty in moving natural limits. That ends in approaching
back breaking resistance from nature, though, and then much too late to
gracefully respond. One can see a possible “Darwinian” cause for
why nature is so full of systems that are highly responsive to soft signals,
then. Organisms and weather systems and lots of other things do, though,
seem to have a way to respond to the approach of limits by completing their
development rather than extending their development to points of failure.
The rarity of complex systems that delay their responses to the last
opportunity might be because they tend to not survive. It’s certainly
true in business and personal relationships, that the
people insensitive to emerging lines of conflict and the need to adapt to
change around them don’t tend to prosper. Perhaps that’s also why what we
mostly see in nature are kinds of systems that respond to real limits at their
earliest opportunity. The implied principle for modeling is that for
models to sensitize us to the need to change assumptions in the future, models
should include leading questions for when to look for information beyond the
model.
For
our present situation the standing world plan for economic growth to multiply
wealth forever includes the design of all our institutions being organized for
that, rather than sensitized to steer away from that. If, say, this is
the first moment the real necessity of that is being noticed, the rational
response would then be to first ask how and when, and the observation that it
seems we are already too late to do it smoothly. Those are things you can
know without knowing very much, is the point. These questions naturally
deserve longer discussion than is possible here. One way to begin exploring
the physical system for answers is to ask what new conditions it’s parts will run into, and look for the things that would
disrupt its positive feedback mechanisms. Those mechanisms will be partly
identified by anything that increases by %’s.
Without even knowing what they are, one can conclude as you identify them that
the question is how it would be best to have them end. Using energy to
multiply our uses of energy and using money to multiply our uses of money to
keep track of what we do with energy both display the basic features of
positive feedback mechanisms and so pose the question of how to end them.
Responsive steering would mean being prepared to end them in a constructive way
at the right time, to avoid having them end disruptively.
4. Conclusion
Learning
much better how to also shape our way of thinking to fit nature’s, relying less
on increasingly controlling nature to fit our own logics and values,
seems to be a necessary part of successfully responding to even our own
designs on earth. Perhaps the time has come when people can finally
understand the formal value of maintaining two explanatory worlds in our minds,
one of connections within our information and one of questions about things
beyond our information. We have actually lived with those two worlds in
our minds all along, of course, while often confusing things by treating them
as one. One gives us our cultural world of meanings that occupies most of
our thoughts mentally, and the other is made of our questions pointing to a
physical world of natural systems we live in physically. Learning to
separate them provides a possible way to understand their connection, having a
use for a world beyond our real understanding supporting an awareness of how
separate that reality is from our own explanations of things. Science
would seem to clearly need both, at least, and the difference in perception
might also be of use to the other parts our own personal and cultural worlds of
arts, values and relationships
6.
Acknowledgments
Considerable
help in this work was provided by years of correspondence with Stan Salthe as
well as many other valued critical thinkers who offered me their time,
attention and insight.
Supplemental
Resources
1. An appendix of theoretical issues & added references cut from this edit. http://www.synapse9.com/pub/ModelsLearningChange-ref.htm
References
Elsasser,
Walter, 1987. Reflections on a Theory of Organisms - Holism in BiologyJohns Hopkins
- found that the persistence of diversity in natural form (heterogeneity) would
conflict with the assumption of statistical causation that underlies
mathematical science.
Henshaw,
P. F., 2010. Complex Systems - Encyclopedia of the Earth
http://www.eoearth.org/article/Complex_systems
Henshaw, P. F., 2007. Notes - Mathematical tests for punctuated equilibrium in draft plankton evolution paper “ Flowing processes in a punctuated species change” http://www.synapse9.com/GTRevis-2007.pdf
Henshaw, P. F., 1999. Features of derivative continuity in shape. Journal of Pattern Recognition and Artificial Intelligence (IJPRAI), Special issue on Invariants in Pattern Recognition, V13 No 8 1999 1181-1199 http://www.synapse9.com/fdcs-ph99-1.pdf
Henshaw, P. F., 1985. Directed Opportunity, Directed Impetus: New tools for investigating autonomous causation. Proceedings; Society for General Systems Research 1985, Louisville KY http://www.synapse9.com/DirOpp.pdf
Rosen, R.,1991. Life Itself. Columbia Univ. Press
Rosen, R., 1993 On The Limitations Of Scientific Knowledge, in: Casli, J. L. (Ed.), On The Limits To Scientific Knowledge. Perseus Books
Salthe, S., 1993. Development and Evolution: Complexity and Change in Biology, MIT Press.
Sterman, J.D., 2002. All models are wrong: reflections on becoming a systems scientist. Jay Wright Forrester Prize Lecture. Syst. Dyn. Rev., 18, 501–531 http://web.mit.edu/jsterman/www/All_Models_Are_Wrong_(SDR).pdf
![]() P. F Henshaw synapse9.com
P. F Henshaw synapse9.com