Appendix to " Models Learning Change" - P.F. Henshaw

Feb 2010

References to Add  & Prior Added Notes Cuts from Models Learning Change

Appendix I.
(sections removed from Sep 2009 draft to be reincorporated perhaps along with continually accumulating notes...)

A.  Distinguishing between information and things

It also takes time to understand how it can be meaningful to discuss physical systems as existing beyond our information, having their own organization embodied in their own structures, and independent of the logic and patterns we see in them.  If one attempts to refer to features of natural systems (local organization accumulating around the movement of energy) beyond what are visible, the question is if they are not visible how do you then refer to them at all.  What is used to connect these apparently separated worlds of mental and physical systems, and resolve the subject/object problem their duality presents, is learning.  Learning is a heuristic mental process that directs attention beyond the knowledge of the learner toward the experience of things in the physical world from which you learn. 

Others have considered that any “subject” is necessarily limited to our available information, so any “object” needs to be reduced to information for it to be referred to and meaningfully exist.  This is one way of stating the Copenhagen interpretation of physics and Heisenberg’s uncertainty principle, to say “if you don’t know about it you can’t talk about it”.  The approach here is the opposite, to consider the subject of science as studying things of the physical world beyond our information, by raising good questions about them.  We get our questions from the information we have, from its incompleteness, and by searching for paths of discovery.  That treats the features of the physical world our information implies to exist, beyond our knowledge, as the real subject of science.  Rather than excluding the physical world from our concerns, information is used for referring to it with our questions and following the paths of inquiry we find productive.  That way the ‘real world’ of scientific information (about a virtual physical reality), and the ‘real world’ of physical phenomena (our virtual information constructs of it describe) become connected.  Both then can be considered ‘real’, alternately looking with one for the other.  Questions may abound, but it seems this dual use of the words is also much more in keeping with normal usage than either one.  People who consider only their theories or beliefs as “real” treat the physical world ‘virtual’, while others tend to do the opposite, and most people seem to go back and forth. 

This tension between our incomplete information and understanding the physical systems we are part of that have organization well beyond our information is also complicated by the two often being confused.  It’s a common habit to represent physical systems as being the models and explanations we have deduced from our information about them.  We sometimes have little other way to refer to them.  The phenomenon of light seems to be a well proven reality, but is only known by deduction from other things, for example.  We use our explanation as a “stand-in” for it in our minds, a way to fill in information about the phenomenon wherever that missing information is needed.  Though the phenomenon of light may not change, lots of other things we treat the same way do, and that becomes a problem of functional fixation (blind spot) if our information does not change with them.  Substituting explanations for features of human cultures and environmental relationships is similarly common and useful, but blocks the learning process by hiding the open questions that might be important to ask as environments change.  To keep explanations from being mistaken for their subjects would call for use them to separately refer to the open questions that remain as well as to what we think we know, as by looking through one at the other.  Otherwise there’s a likelihood of confusing the two, substituting simple but wrong explanations precisely where physical systems have their most dense organization and unexpected features.  Table 1 lists major worlds of human information and ideas with their corresponding physical subject, each representing a learning process about organizational processes, the understanding and the doing or things.

Explanatory Systems (information worlds)	Physical Systems (behavioral worlds)
Perception, Reasoning & Belief	· individual learning and experience
Physics	· forces, fields, mass, energy, forms of complexity & change
Economics	· economies, businesses, human behavior
Biology	· organisms
Ecology & Geology	· relations between animate and inanimate parts of environments
Sociology & Anthropology	· human relationships and cultures
Medicine	· practice of health care
Engineering, Architecture, Technology	· practice of design
The Arts	· practice of crafts
Culture, Business, Government	· practice of organization

Table 1.      Short list of mental disciplines with corresponding physical subjects

Mistaking mental and physical systems might be less of a problem if the two kinds of organization, mental and physical, were similar in kind.  Mental models and physical systems are remarkably different, though, such as one being scale dependent and the other not.  It is also interestingly difficult, for example, to determine if what happens inside natural systems is deterministic as it sometimes appears, or if parts act in a way that is truly opportunistic as it also sometimes appears, or a mixture.  The more information we have the more it appears we can determine, as if projecting a state of having limitless information would mean being able to determine everything.    It is also precisely the interior designs and behaviors of complex systems that are most opaque to study, and for which so very little can be determined, that do appear to represent individuals truly behaving opportunistically.  It’s as if the interiors of the more complex natural systems are distinct holes in an information world made like Swiss Cheese, where natural system organization is most densely concentrated in what look like voids.  If true, the substitution of simple deterministic explanations to fill these voids of understanding, about self-organizing and self-animating things, would result in a particularly large misrepresentation. 

In either case correcting the error of letting your own information become confused with the subject it is about then allows some comparison, and making the differences between them useful.  Failing to do so makes explanations self-referencing and become just a collection of conventions instead of information about any other thing at all.  If in addition systems that were opportunistic are then represented as deterministic what is lost is even the concept of their having their own original behavior and reactions, learning and internal world.  Keeping them mentally separate, our dual physical and information worlds, may not be automatic or easy but considering the information as an overlay, is then just a matter of shifting attention when needed to the unanswered questions underneath.

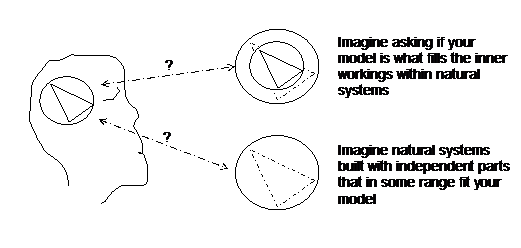
Fig.  1  Are our models what nature uses to operate?   If not, does keeping the two separate help or hinder?  Does using models to fill voids in our understanding of nature hide anything that turning them into questions would illuminate?

B  Why physical things remain undefined

Natural systems, like storms, organisms or cultures, take care of themselves and work by processes seemingly inside themselves that remain largely invisible.  but    One great difference from our theories is that these and many other kinds of natural systems appear to be significantly opportunistic in their behavior, as if probing their environments to seek out new directions to develop.  How that might occur is hidden within their complex and changing forms, making any line between opportunistic and deterministic behavior unclear.   Having it hard to see how they work does not keep one from watching for warning signs for when they will change direction though, or find a few reliable regularities.  Watching them change direction helps locate where they are too, and then some of our considerable native understanding of them that is part of natural language can be used.  The subject of natural systems actually seems to be the main subject of natural language, one or another way.  There’s hardly any topic of conversation that doesn’t concern one or another kind of leaderless network of relationships, with real properties and consequences for us personally.  Many common words refer to them and their general properties.  Natural systems are the subject of anything one might refer to as “established” or “on track” or “off track” or “coming to a head”.  It also refers to natural systems to discuss most anything as having “relationships” or as “growing” or “developing”. 

Natural systems tend to be cohesive, but among the many reasons it is quite hard to follow how they work is that, like in your body, the activity and parts of such networks of connection are changing everywhere all the time.  That means that wherever you look nearly all the real action is located somewhere you’re not looking.  Still, with many kinds of complex natural systems the closer you look you don’t find chaos.  You more often find more scales of exquisitely organized processes arranged in leaderless networks, with similarly distributed changing parts.  The individuality of natural systems is another aspect of them that is stubbornly resistant to explanation, the appearance that no two physical things are ever made alike.  That what theoretical constructs are based on is exact and completely unvarying replication, rigid rules of logic, points to another basic difference between them. 

A number of other scientists studying the relation between systems of equations and physical systems have also reached the conclusion that natural systems actually can not be validly modeled, or if they were their models would be ‘incomputable’.  Walter Elsasser (1987) found that the persistence of diversity in natural form (heterogeneity) would conflict with the assumption of statistical causation that underlies mathematical science.  Robert Rosen (1991) showed that modeling systems would at minimum require infinite regressions that no machine could perform and so nature could not be a machine or modeled by one.  Rosen (1996) also observed that living systems seem to incorporate divergent series of changes and scientific models can only be usefully defined using convergent mathematical sequences.  In addition various systems scientists such as John Sterman (2002) have observed that “All models are wrong” for a combination of causes ranging from natural human failings, to the deep complexity and profound lack of information about most kinds of complex systems of interest.  These all point to modeling failures as being largely for natural causes, a difference between the subject and our information.

These observations on the fundamental problems of why models fail were essentially cautionary, though, rather than providing improvements on any method for modeling complex systems.  Not to diminish the value of any of the extensive efforts of others in finding regularities that a mathematical model could be reliably be built around, the approach here is to identify predictable irregularities, identifying where models are about to need to change.  It could be seen as an application of Rosen’s later observation, that nature is full of what appear to be divergent sequences of development, for which useful equations can’t be defined.  Looking at what nature can do that math cannot do, and for what math can do that nature cannot, provides a way to connect them through the questions about how they differ, and use each to learn about the other.  The method introduced in section 3.  uses a family of implied violations of the conservation laws that physical systems are subject to but mathematical systems are not.  They generate very useful questions about when modeling will need to go beyond the available information to discover what new assumptions will be needed.

C  Connections between natural systems and formal systems.

Presented world

Learning to coordinate systems different in kind

Re-presented world

Fig.  2 – Natural & Formal Systems - Robert Rosen 1991 with added notes

Fig.  2 is Robert Rosen’s diagram of the relation between natural and formal systems, how the theoretical world is assembled (encoding) and used to guide us (decoding) in navigating the physical world .  In addition to the difficulties of making good models that Sterman and others identify, there are some very odd features of physical causality that models could never be made to emulate.  Natural systems are all individually different and continually changing everywhere at once, with each part changing differently.  Any model that did that would not compute.  Our ability to describe physical things requires using general categories and statistical uncertainty, but physical subjects are not composed of categories, and also appear to be completely particular in every detail, apparently having no ambiguous feature of any kind except for the ambiguity faced by an observer in how to describe or explain them.  Natural systems also have multiple scales of differently organized parts.  Their multi-scale networks of separately changing parts are held together by interacting through and with their environments, and so are not at all self-contained or self-consistent in design.  Information about any part will very predictably omit relevant information about the other scales of organization around and within it. 

Mathematical models rely on fixed definitions and complete information, though, having none of those odd features of nature.  Mathematical models need to be self-contained and self-consistent because they have nothing to hold them together but logic and the abstract definitions the logic connects.  Models rely on natural regularities of unknown origin, but there’s a flaw in relying on them if we don’t understand something about where and when they might change. 

In the process of observing and formalizing natural systems people reduce nature to information.  We record information by counting individual physical events and the results of periodic measures grouped in defined categories, using a mix of fairly narrow as well as broad and loose definitions.  Sometimes we keep track of whether the measures we use are of conserved change in accumulative processes or non-accumulating indicators, and sometimes not, and represent changes in one as factors for the other.  Our information categories are not naturally connected, in general, other than how we use them..  Consequently it can be quite unclear what we are measuring and what it is information about except the conventions of normal practice.  We also may not think that our categories change, for example, but nature may fill them with all kinds of changing things, even if we use the exact same procedure for collecting data for them over and over.  For a simple hypothetical example, you may ask a standard interview question one year, and find that the words have changed meaning the next, or try to track the price of a standard “market basket of goods” to find later that no one buys those things anymore.  That nature is not as confused as the arrangement of our information is sometimes only evident in what Elsasser described as “persistent heterogeneity” or Rosen as “life”, the evident continuities displayed in our separate categories of information  that seem associated with the continuity of entire systems beyond our description.  A great many of the natural systems displaying real continuity that concern people are full of independently learning and responding parts, like economies and ecologies, that are both highly complex and evidently take care of themselves.  Reading those continuities, as evidence of implied natural systems, and their systematically diverging relationships as evidence of approaching change helps point to where and how it will occur, and the need for connected formal explanations, whatever their arrangement is, to adapt.

Having signs of when they will change would be a way to study how natural systems are so very effective in taking of themselves, without controls, clearly displaying methods of very efficient cooperation in many ways.  There is a strong similarity between how neatly the parts of many kinds of natural systems fit together and provide complementary services to each other.  The wastes and inadequacies of one part often serve as resources and opportunities to develop for others.  If the parts of natural systems were actually opportunistic, that could well explain that odd feature.  Opportunistic systems would use what they find free to take, fill in where there are gaps, avoid conflict as a waste of energy.  It would also explain the coincidental similarity between how economic markets link complementary talents and businesses and the way natural environments are similarly assembled from complementary parts and functions, if nature’s main method of creating systems were similar to the way people make their livings.  If so it would provide a new diverse group of physical models of more successful kinds of economies that don’t build to collapse, for studying how .  

D Reading beyond one’s information

That learning pushes you find ways to read beyond one’s information, and relate to physical things and relationships that may remain partly out of view, takes also being cautious to not jump to conclusions.  Hypotheses need some testable foundation.  A “hypothesis” is itself a cautious reading beyond one’s data in search of evidence.  Even representing nature with equations, for example, is by itself a leap of faith in representing complex physical things with a symbolic construct and implies a “reading beyond the available data” that we choose to rely on.  Identifying progressions that will be certain to upset the system of relations they are part of is then just another kind of valuable information about things presently hidden, an open question with a solid foundation.  Discovering evident gaps in explanations, such as energy densities implied to approach infinity or zero has led to numerous discoveries of physics.  The discovery of atoms and atomic particles partly resulted from trying to explain how to avoid unlimited electric field densities.

Still, referring to things that have yet to be discovered, and are known mainly by something clearly being missing from view, can easily be confusing.  Common language has a way to do it, by just pointing to undefined physical things with names,  For many of the unusual forms of natural systems and their organization there are as yet no names, nor a good way to point.  What seems clear is that our own very limited logical constructs for them are clearly organized in a rather different way.  I will propose some terms and uses, but those who prefer to be cautious might continue to begin from the presumption that individual physical systems are always undefined and actually contain nothing to directly inform us themselves.  Some others, perhaps the “agnostics” may then wish to follow that by a ? mark, asking that statement as a question.  At the very least I think it’s it appropriate to always continue to refer to the physical organization of natural systems hypothetically.  What people find inside the workings of natural systems, say looking inside a human body or trying to understand what water is, continues to fill books of facts and remain inexplicable.  If what we see from the outside of any locus of organization has some predictable regularity, we still generally don’t know quite where it comes from and so may never quite know when it will change.

That we have a natural way of pointing to natural systems without specifying exactly what is being pointed to at is a start can be improved on.  The existence of their interior designs of many kinds of natural systems is evident from how they change everywhere at once, using multiple nested scales of organization, changing scale and form at the same time with no apparent communication from elsewhere.  Something holds together their great networks of separately developing and adapting parts, interacting with others through environments with undefined boundaries.  Equations of controlled variables can’t do that and asking why real and formal systems differ is a way asking productive questions.  If one of the main features of natural systems is their inexplicably complex and smooth operating interior designs, one place to start is observing that to us they seem organized around  a “wilderness of unknowns”, definite realities that remain “undefined and unexplored”.  Thinking of the “envelope” of all that is possible to explain, individual natural systems each represent significant holes.. 

Nature is an exemplary organizer and builder of vaguely machine-like systems.  The numerous systematic growth processes that smoothly develop exceptionally complex things with only the process and an environment of loose parts to account for it is a primary example.  That is so very different from how logically defined and controlled systems operate that the problem may not be that we have not yet found how natural systems are organized, but that they may not actually have any of our kind of definable organization at all.  It may not then “explain” them, but just be very helpful for making models we can trust to be able to tell when natural systems are changing form and new assumptions for our models will be needed.  The object here is then to define some limited ways to predict when and how our models will become undefined, and point to learning paths for finding new assumptions to make and accommodate the natural changes taking place. 

E Raising questions of change

animated glove?	animated world?
animated hand?
animated cup?

Fig 3                       Which wholes does one choose to model?

The “null hypothesis” here is that trustworthy theories reflect some regularity of the complex physical world beyond their information and so do not contain information about the range of their own validity.  For questions about the limits of their validity someone would need to look into the gaps in their information.  So in order for models to imitate natural systems and adapt to their environments as natural systems do, models would need their makers and users to do the learning needed and change them.   What requires the learning is not that modelers are not proficient in emulating any form of behavior that can be specified.  It’s that we cannot specify behavior beyond our information, particularly if it concerns natural systems which themselves may be learning processes or self-animating.  If you consider a model (fig.  3) as an animated glove, designed to emulate the animated hand of nature, it may not contain information about whether or not the fingers in the glove or the cup held by the hand are connected. 

If the regularities of the physical system taken to be constant were to change, or “come alive” as it were,  then the assumptions of the model would become invalid leaving the model and perhaps the purpose it was designed for undefined.  Technology change frequently presents this kind of problem of basic changes in relationships that were once assumed constant and unexpectedly redefine the meaning of the questions people have.  The changing scale of our economic footprint on the earth does as well, forcing a general rethinking of the purpose of development and our relationship with the earth.  If you know that’s coming it has the effect of turning the “=” signs into “?” marks, in time to learn how to change the model before it fails..

For example, the usual way models of growth and climax are defined, say in maximizing the use of a limited resource, is with a logistic curve.  That approximates the transition from positive feedback in seed growth followed by negative feedback in responding to limits with one continuous equation.  Clearly in nature those are often two separate and distinct processes operating by two very different kinds of systems of response.  In particular, the constraints of natural limits do not begin with the first use of a seed resource.  As a seed resource is uses systems are self-limited as they develop their ability to use what is plentiful , but as the demands of the growing system exceed it’s available resources and force it change what it is responding to.  That means that in nature there is a break in the middle of the sequence where the responses of the physical system to one thing end and to another thing begin, a discontinuity.  That means it’s possible that any logistic curve mistakenly represents a succession of different systems as a single system, and skips over the organizational discontinuity between them.  In that case the inflection point in the response curve from growth to climax  possibly needs to be read as a question mark (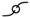= ?) about what physical system change the missing discontinuity in the equation represents.  The system starts with quite different boundary conditions than it ends with. 

Logically, of course, a system can’t have information about its end before its beginning, any more than a car fender would be starting to bend for the tree it will hit as soon as the car heads toward it.  So there must be at least two periods of regularities with different equations, not one, with new information needed about what will change to define the transition.  What is then clearly missing from logistic curves is the point or period of time in which changes to the assumed regularities of the system beyond the information of the model occur and begin following new boundary conditions..  Therefore some system changing event occurs, due to change in features of the physical system beyond the information of the model.  They might be either within the system or its parts or in the environment in which it operates, or both. 

Examples abound of natural systems that begin with unconstrained growth brought to an end by some internal change rather than some external bound.  Organisms generally mature to some optimal size for their life ahead rather than being limited by exhausting their environments.  Air currents and drips of water are also self-limiting in how they develop, coming to points of development where they separate from their sources rather than continuing to develop to the exhaustion of their sources.  Externally limited processes are common as well too, as well as systems that exhibit a combination of internal responses to external limits, such as animals foraging and searching for food as they also seek to avoid danger, or crystal formation or bee hive designs based on modular elements that are replicated to consume other natural limits.

Often times one can tell from a model that the development of a system will be limited, though the model won’t say how exactly.  If the change in boundary conditions and behavior in switching from growth to climax in natural systems takes place due to a combination of internal and external forces, many of which could involve complex behavioral systems on other scales, what is happening is more complicated than an equation.  You then have one complex process coming to an end and setting the stage for the next.  What determines how the change will occur is made by interactions between elements within and around the originating system that are unprecedented.  Studying a model for where these are implied to take place as if inserting question marks into the models for “what’s happening here ?” then helps locate and discover them.  It's "raw science" not "finished science", and intended as a way to extend either beginning or advanced research into any field by raising new kinds of focused questions about changing environments.  It's also a way to open our minds and learn how to follow nature's actual processes. 

At first the ability to follow successions for system states takes time to develop, but we also all have somewhat highly developed skills for it in areas of personal experience.   Many of the same kinds of questions about when developmental stages will be changing apply very broadly.    Raising children, for example, exposes you to a succession of natural stages of development that are temporarily stable.  As change from one to the next approaches it exposes threads of new questions and issues that  both parent and child need to follow to be able to make the successions from one world of relationships to the next.  Sometimes such changes catch either parent or child off guard as circumstances race ahead of preparation for them.  Sometimes they’re prepared for long ahead.  The same would apply in not an entirely dissimilar way to the issues surrounding the maturation of lots of other kinds of growth systems, a business, a whole civilization, or single projects that start from scratch like a group of kids learning a school play.  Each of these are of different kinds and on different scales but of the sequence of developments has many things in common.  

Appendix II. References

A. References to add - 2/4/10

Peter M. Allen 2010 Editorial, Emergence Complexity & Organization, 11-4 2009
- "In an evolutionary universe, we are destined to continue a perpetual learning process without end [as does our environment] as we develop, correct and adapt our interpretive frameworks to gradually fossilization which, fortunately, we then fail to pass on to the next generation."

TFH Allen, JA Tainter, J Chris Pres, TW Hoekstra 2001 Dragnet Ecology - "Just the Facts, Ma'am": The Privilege of Science in a Postmodern World BioScience, v 61-6
- narrative as the art of science

Brian Goodman 1994 How the Leopard Changed its Spots. Princeton Univ. Press

W. Richard Scott 3003 Organizations, rational, natural and open systems, 5th Ed., Prentice Hall

B. Prior References

Elsasser, Walter, 1987. Reflections on a Theory of Organisms - Holism in Biology Johns Hopkins
- found that the persistence of diversity in natural form (heterogeneity) would conflict with the assumption of statistical causation that underlies mathematical science. 

Elsasser, Walter, 1966 Atom and Organism - A new approach to Theoretical Biology, Princeton Univ. Press.

Henshaw, P. F., 2010. Complex Systems. Encyclopedia of the Earth
http://www.eoearth.org/article/Complex_systems  

Henshaw, P. F.,  2007. Notes - Mathematical tests for punctuated equilibrium in draft plankton evolution paper “ Flowing processes in a punctuated species change” http://www.synapse9.com/GTRevis-2007.pdf

Henshaw, P. F., 1999. Features of derivative continuity in shape. Journal of Pattern Recognition and Artificial Intelligence (IJPRAI), Special issue on Invariants in Pattern Recognition, V13 No 8 1999 1181-1199 http://www.synapse9.com/fdcs-ph99-1.pdf

Henshaw, P. F.,  1985. Directed Opportunity, Directed Impetus: New tools for investigating autonomous causation. Proceedings; Society for General Systems Research 1985, Louisville KY http://www.synapse9.com/DirOpp.pdf

Rosen, R.,1991. Life Itself. Columbia Univ. Press
- showed that modeling systems would at minimum require infinite regressions that no machine could perform and so nature could not be a machine or modeled by one

Rosen, R., 1993 On The Limitations Of Scientific Knowledge, in: Casli, J. L. (Ed.), On The Limits To Scientific Knowledge. Perseus Books
- also observed that living systems seem to incorporate divergent series of changes and scientific models can only be usefully defined using convergent mathematical sequences. 

Salthe, S., 1993. Development and Evolution: Complexity and Change in Biology, MIT Press.

Sterman, J.D., 2002. All models are wrong: reflections on becoming a systems scientist. Jay Wright Forrester Prize Lecture. Syst. Dyn. Rev., 18, 501–531  http://web.mit.edu/jsterman/www/All_Models_Are_Wrong_(SDR).pdf

Appendix III. Added Notes

2/4/10 - Once sorted a bit, none yet...